| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 컴퓨터 구조
- Air Table
- 수학
- 접미사 배열
- jpa
- JavaScript
- Cloud Run
- Bit
- 시뮬레이션
- 생활코딩
- BFS
- 펜윅 트리
- 고속 푸리에 변환
- REACT
- 백준 1753번
- ICPC
- 우선순위 큐
- LCS
- 이분탐색
- Cloud Pub/Sub
- 다이나믹 프로그래밍
- 다익스트라
- 삼성SW역량테스트
- 종만북
- r
- 데이터 분석
- dp
- 삼성 SW 역량테스트
- CI/CD
- 그리디
- Today
- Total
코딩스토리
Longest Common Subsequence (LCS, 최장 공통 부분 수열) 본문
오랜만에 블로그에 알고리즘 관련 글을 작성하는 것 같은데..
절대 알고리즘에 손을 놓고 있던 게 아니라 우리 학교 알고리즘 소학회에 참여하느라 ㅎㅎ..
( KOALA 뽜이팅!!)
LCS 알고리즘은 DP를 공부했던 시점부터 계속 공부해야지, 공부해야지 했던 알고리즘인데 결국 오늘에서야 공부했다.
( 다음 주 학회의 주제가 마침 DP여서도 있고 )
어쨌든 LCS 알고리즘에 대해 알아보면
Longest Common Subsequence, 즉 최장 공통부분 수열이라는 뜻이다.
만약 ACAYKP 란 문자열과 CAPCAK 란 두 개의 문자열이 주어졌을 때,
LCS = ACAK 가 된다.

최장 길이 문자열과 살짝 헷갈릴 수 있는데, 우리가 구해야 하는 LCS는 최장 부분 공통 수열, 즉 수열이다.
수열이란 뜻은 결국 이어져 있지 않아도 된다는 얘기다. (연속하지 않아도 된다.)
그럼 이 LCS를 어떻게 구해야 할까?
가장 단순한 방법을 생각해보면, 각 문자열이 만들 수 있는 모든 부분 수열을 구해서 비교한 뒤 가장 큰 값을 찾아내는 방법이 존재할 것이다.
이 방법은 각 문자열의 길이가 n, m이라 가정했을 때 O(2^n * 2^m) 이란 무지막지한 시간 복잡도를 가지게 된다.
(길이 n짜리 문자열에서 모든 부분 수열을 만드는 시간 복잡도는 nC1 + nC2 + nC3 +... + nCn-1 + nCn = 2^n 이므로)
2^n 이거 하나만으로도 문제를 푸는 입장에서는 매우 매우 부담인데 두 개의 곱이란..
사실상 이 방법으로는 해결하지 못하는 것과 다름없다.
그래서! 우리는 이 과정에서 다이나믹 프로그래밍을 사용하여 시간을 확 줄여줄 것이다.
먼저 LCS를 이해해 보자면
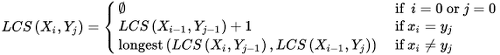
총 3가지의 경우로 나눌 수 있다.
( 여기서 Xi란 X 문자열의 첫 번째 index부터 i번째 index까지의 문자열이다. 밑의 표를 보면서 이해하면 쉽다.)
1. i = 0 or j = 0이라면 LCS(Xi, Yj) = 0이다.
이 부분은 아래에서 보면 더 이해가 잘 가겠지만 2,3 번째 조건을 편하게 사용하기 위해 있는 조건이다.
( 스포 하자면 3번째 조건의 Yj-1, Xi-1의 영향을 받기 때문에 정확히 말하면 i = 1, j = 1 일 때를 위한 조건이다.)
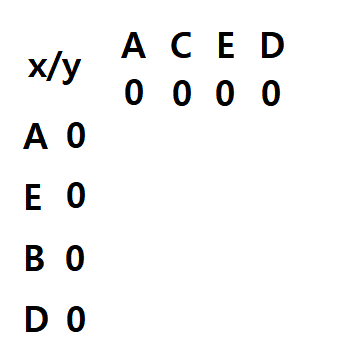
2. xi = yj 라면 LCS(Xi, Yj) = LCS (Xi-1, Yj-1) + 1이다.
이 조건은 처음 보면 직관적으로 이해하기 어렵다.
왜..? 왜..? 나도 이 말만 10번은 되새겼던 것 같다.
다들 나랑 비슷하겠지만 왜 Xi-1, Yi-1에 접근하는 거지?
지금부터는 내가 이해했던 방법을 소개해볼까 한다. ( 정확하다고 말할 순 없겠지만.. 아마도 맞을 거예요 ㅎㅎ)
먼저 X = AEBD라고 하고, Y = ACED라고 하자.
위에서 언급했듯이 Xi란 X 문자열의 첫 번째 index부터 i번째 index까지의 문자열이다.
그리고 xi = X 문자열의 i번째 index의 문자이다.
그럼 LCS(X2, Y3) 를 한번 구해보자.
x2 = y3 인가? YES!! (x2 = 'E', y3 = 'E')
그렇다면 위의 식에 따라 LCS(X2,Y3) = LCS(X1, Y2) + 1 일 것이다.
이제부터 살짝 마법을 부려보면 (써놓고 보니 되게 유치하네요ㅎ)
X2, X1 이런 것들을 문자열로 바꿔보자. 그러면
LCS(AE, ACE) = LCS(A, AC) + 1이다.
이제 조금 보이지 않나요? 나만 보여요?ㅠㅠ
이렇게 고쳐놓으니 직관적으로 해석이 가능해진다.
AE란 문자열과 ACE란 문자열의 LCS를 구하고 싶다면, 그 전까지의 문자열 A와 AC, 이 두 문자열의 LCS를 구한 뒤 + 1 하면 된다는 것이다!
( 'E'가 같기 때문에 + 1 이 되는 것이다.)

충분한 설명이 되었는지 모르겠지만.. 그래도 일단은 세 번째 조건으로 넘어가 보자.
3. xi!= yi 라면 LCS(Xi, Yi) = longest(LCS(Xi, Yj-1), LCS(Xi-1, Yj))이다.
이게 무슨 소린가.. 겨우 2번을 이해했더니 이건 또 무슨 더러운 식이지..
B.U.T
우리는 할 수 있다. 왜냐? 위에서 했던 방식 똑같이 하면 된다.
위와 똑같은 예제로 해보자.
먼저 X = AEBD라고 하고, Y = ACED라고 하자.
LCS (X3, Y2)를 구해보자.
x3!= y2이다. ('B'!= 'C')
그럼 이걸 3번 조건식으로 나타내 보면 LCS(X3, Y2) = longest(LCS(X3, Y1), LCS(X2, Y2))이다.
보기만 해도 어지러우니까 바로 바꿔보면
LCS(AEB, AC) = longest(LCS(AEB, A), LCS(AE, AC))이다.

현재 비교하는 문자가 다르기 때문에 이전까지 만들 수 있는 모든 부분 수열 중 최댓값을 가지고 가야 한다는 것이다.
근데 그 부분 수열들의 최대값을 어떻게 구할 것인가가 문제가 되는 거겠죠?
바로 이 부분에서 DP가 사용되는 것이다!
(LCS를 DP라고 바꿔 놓고 생각해보면 정말 놀랍게도 그냥 DP문제예요.. 이게 말이 되냐고!!)
자 이제 3가지 조건을 다 살펴보았으니 우리는 이제 LCS를 구할 수 있다.
LCS를 DP 배열로 생각하고 각 조건에 맞게 코드를 짜면 된다.
for (int i = 1; i <= A; i++) {
for (int j = 1; j <= B; j++) {
if (a[i - 1] == b[j - 1]) {
LCS[i][j] = LCS[i - 1][j - 1] + 1;
}
else {
LCS[i][j] = max(LCS[i - 1][j], LCS[i][j - 1]);
}
}
}
조건을 C++로 고대로 옮겨놓았을 뿐이다.
결국 우리가 구해야 할 LCS(X, Y)는 LCS [X.size()][Y.size()]에 담겨있다.
내가 이 글에서 꼭 얘기하고 싶은 점은 무작정 LCS는 왼쪽 대각선 + 1! 이렇게 외우지 말자는 것이다.
물론 문제를 풀 때에는 가장 도움이 되는 방법이긴 하겠지만 분명 까먹는다. 100% 1000% 까먹는다.
그렇기 때문에 시간이 조금 걸릴 순 있어도 꼭 어떤 방식으로 LCS를 구하는지 이해하고 넘어가는 게 중요할 것 같다.
(다른 블로그 글들을 찾아보니 생각보다 그냥 점화식으로 설명을 끝내는 경우가 많은 것 같아서..)
관련 문제 : 백준 9251번 LCS
해설 : kimtaehyun98.tistory.com/63
백준 9251번 - LCS
www.acmicpc.net/problem/9251 9251번: LCS LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, ACA..
kimtaehyun98.tistory.com
'알고리즘 > 알고리즘 공부' 카테고리의 다른 글
| Binary Index Tree(BIT, Fenwick Tree) (0) | 2021.05.28 |
|---|---|
| 확장 유클리드 호제법 (3) | 2021.05.25 |
| 트리 - 우선순위 큐와 힙 (0) | 2020.10.02 |
| 문자열 - 맨버 마이어스 알고리즘 (0) | 2020.09.13 |
| 문자열 - KMP 알고리즘 (0) | 2020.09.09 |



