| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 삼성SW역량테스트
- Cloud Pub/Sub
- REACT
- r
- 접미사 배열
- BFS
- LCS
- 그리디
- 삼성 SW 역량테스트
- Bit
- jpa
- 시뮬레이션
- 수학
- 생활코딩
- 데이터 분석
- 컴퓨터 구조
- dp
- 펜윅 트리
- 백준 1753번
- Cloud Run
- ICPC
- 고속 푸리에 변환
- 종만북
- 우선순위 큐
- CI/CD
- JavaScript
- 다익스트라
- Air Table
- 이분탐색
- 다이나믹 프로그래밍
- Today
- Total
코딩스토리
Chapter 6. 연산장치 본문
# 본 내용은 한국항공대학교 길현영 교수님의 '컴퓨터 구조' 강의 및 컴퓨터 아키텍처(우종정, 한빛 아카데미)를 바탕으로 작성한 글입니다.
연상 장치에 대해 공부하기 전 디지털 논리회로 시간에 배운 것에 대해 간단하게 복습해보자.
디지털 논리회로 Review
데이터/연산의 HW 구현
데이터 : 전기신호의 흐름을 기호화
연산 : 논리 게이트를 기본 단위로 하여 해당 연산 결과를 구할 수 있는 디지털 논리회로 구축 (AND, OR)
논리 게이트
논리 회로의 기본 HW 소자로 입력 단자의 값에 따라 해당 논리 게이트(연산)의 논리 값을 출력 단자의 값(0, 1)로 출력
조합 논리회로
현재의 입력값에 의해서만 출력 값이 결정, 저장장치 없음 (가산기. 비교기, 디코더, 인코더, MUX 등)
순차 논리회로
저장장치 존재, 저장장치 내 상태(state)가 존재하기 때문에 Sequence 구현이 가능
출력 = 현재의 입력 + 기억소자의 state값
디코더
출력 단자 중 하나만 1로 출력
입력 단자가 n 개라면 출력 단자는 2^n 개다. (디논 시간에는 출력을 늘려주는 회로라고 배웠던 것 같음)
인코더
디코더와 반대의 기능.
입력 단자 중 하나만 1이며 출력의 개수를 줄여주는(정확히 말하면 n개에 맞춰주는) 장치이다.
입력 단자가 2^n 개라면 출력 단자는 n 개다.
멀티플렉서 (MUX)
다수의 입력 단자 중 조건에 맞는 하나를 선택하고, 단일 출력하는 조합 회로이다.
기말 시험에도 문제로 나왔던 개념이라 아직도 기억하고 있다..
디멀티플렉서
하나의 입력 단자를 다수의 출력 단자로 연결
반가산기 (Half Adder)
1비트 단위의 덧셈 수행 : 결과값으로 s와 carry를 내보낸다.
전가산기 (Full Adder)
올림수까지 포함해서 2비트 이상의 덧셈 수행
디논 시간에 배웠던 것들이기 때문에 간단하게 어떤 건지만 복습하고 넘어갔다.
1. 연산장치의 개요
CPU는 기본적으로 제어장치와 연산장치로 구성되며, 그 외에 레지스터, CPU버스 등을 포함하고 있다.
연산장치는 산술논리장치(ALU)를 줄인말로 실행 장치라고도 한다.
연산장치는 덧셈, 뺄셈 같은 산술 연산과 AND, OR 같은 논리 연산을 수행하므로 산술, 논리연산기를 기본적으로 가지고 있으며 시프터, 보수기 등도 포함한다.
연산장치는 CPU 내부에 위치하고 있기 때문에 레지스터 파일에서 데이터를 가져오고, 데이터를 저장한다.
우리는 PicoMips 아키텍처를 사용하여 공부하고 있기 때문에 잠시 살펴보면 아래와 같다.

처음 이 사진을 보았을 때는 뭐지? 하고 넘어갔는데
뒤로 가서 공부할수록 얼마나 중요한 사진이었는지를 깨달았다..
설명해보자면 picoMips 아키텍처에서는 r, i, j 형식 명령어가 있는데 각각에 따라 레지스터의 주소가 들어올 것이다.
입력된 레지스터 주소와 연산 부호에 따라 데이터를 ALU에 넘겨주고 ALU는 연산한 결과를 레지스터 파일에 입력한다.
ALU는 산술 연산과 논리 연산이 둘 다 가능하다.
산술 장치와 논리 장치를 MUX를 이용해 연결하여 사용한다.
2개의 16 bit입력 데이터가 산술 장치와 논리 장치에 입력
• 입/출력 올림수는산술 장치에만 각각 입력되고 출력
3 bit의 제어신호는 연산 종류와 출력 선택
• 2 bit는 산술 장치와 논리 장치에 입력되어 각 장치의 연산 종류(각 4개)를 선택
• 1 bit는 멀티플렉서에 적용되어 산술 장치와 논리 장치 출력 중 하나를 출력
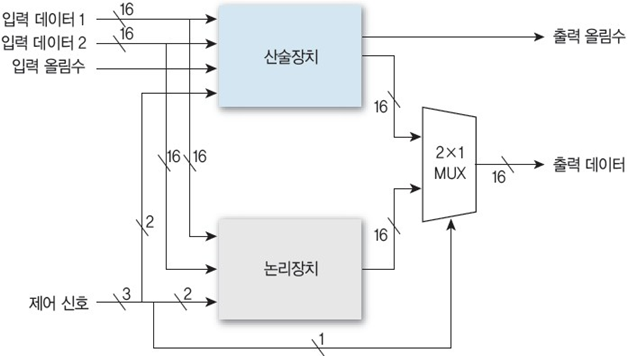
쉽게 말하면 입력 데이터를 산술 장치와 논리 장치에 각각 입력시키고,
산술 장치는 산술 연산을, 논리 장치는 제어 신호에 따라 논리 연산을 진행한 뒤 MUX를 통해 출력 값을 하나만 선택하여 내보낸다는 것이다.
플래그 레지스터
CPU 내 연산 과정 중에 발생한 상태를 보관하기 위한 특수 기억장치
올림수(C), 오버플로우(V), 부호(S), 0값(Z)와 관련된 상태 비트를 포함한다.

2. 정수의 덧셈
앞의 '데이터의 표현' 챕터에서 우리는 2의 보수 표현법을 사용한다는 것을 알았다.
그렇다면 2의 보수 표현법으로 표현한 정수의 덧셈과 뺄셈에 대해 알아보자.
덧셈과 뺄셈은 어렵지 않다. 하지만 문제는 더한 후의 결과이다.
먼저 예제를 보자.

정답까지 같이 나와있지만 어쨌든 살펴보면 어렵지 않은 계산들이다.
이때 주의할 점은 결과도 2의 보수 표현법으로 나오기 때문에 결과를 10진수로 생각하려면 바꿔줘야 한다는 점이다.
이게 뭔 소린가 할 텐데
예를 들어 덧셈의 결괏값이 1011이라면, (1011 + 1)을 1의 보수 취한 -5가 답이라는 것이다.
이 예제를 통해서 생각해 볼 수 있는 점은
1. 두 수의 부호가 다르다면 : 절댓값이 큰 수의 부호를 따라가며, 자리올림수(carry)를 무시한다.
자리올림수를 무시해도 되는 이유는 n bit 정수라 했을 때 우리는 앞에서 공부했기 때문에 -2^(n-1) ~ 2^(n-1) - 1까지의 수를 표현할 수 있음을 알고 있다.
따라서 만약 부호가 다르다면, 어떠한 경우에도 범위를 넘어가지 않는다. (매우 당연한 말이다.)
2. 두 수의 부호가 같다면 : 범위를 벗어나는 오버플로우가 발생할 수 있으므로 확인해줘야 한다.
두 수의 부호가 같다면 데이터의 범위를 넘어갈 수 있다. (ex. 4bit의 경우 -4 + (-5) = -9 이므로 오버플로우 발생!)
따라서 오버플로우가 났는지를 먼저 체크해 줘야 한다.
오버플로우 점검
MSB에 대한 입력 올림수 C in과 출력 올림수 C out가 서로 다를 때 오버플로우가 난다!

정수의 뺄셈은 음수를 2의 보수로 바꿔준 뒤 덧셈하면 되기 때문에 다른 HW를 구현할 필요가 없다.
위의 사진은 디논 기말고사 때 직접 구현하는 문제로 나왔었기 때문에 잊히질 않는다..
3. 정수의 곱셈
무부호 정수의 곱셈 : 종이 - 연필 방식

이 그림을 통해 알아야 하는 점은 아래와 같다.
곱셈 결과는 최대 2n bit수 이다!
위는 사람이 직접 연필을 들고 계산할 때의 방법이고 컴퓨터가 계산하려면 그에 맞는 HW를 구현해야 한다.
시프트 - 덧셈 방식 (개선 전)
각 사이클마다 부분곱을 왼쪽으로 1-shift 하고, 누적 부분곱에 부분곱을 더한다.

문제는 부분곱 계산을 위해 2N bit 덧셈 연산이 필요하다는 것이다.
시프트 - 덧셈 방식의 곱셈 연산 (개선안)
아이디어는 다음과 같다.
계산은 앞쪽(상위 N bit)에서만 하고 뒤(하위 N bit)에는 저장만 하자!
이렇게 하려면 부분 곱을 누적시켜 줄 때 상위 N bit에서 계산해서 누적시켜 주고, 오른쪽으로 1-shift 해주면 신기하게도 같은 결과값이 나온다.
장점은 당연히 앞쪽 N bit에서만 연산을 진행하기 때문에 N bit 덧셈 장치를 사용하여 N bit 곱셈 장치를 만들 수 있다는 것이다.

Booth 알고리즘
어렵다..
원리는 아래와 같다.
1번 경우 : A×9999 = A×(9+90+900+900) : 곱셈 4번과 덧셈 3번 필요
2번 경우 : A×(10000-1) : 곱셈 2번과 덧셈(/뺄셈) 1번 필요
두 연산은 사실상 똑같은 연산이다. 하지만 컴퓨터가 계산하는 데에는 2번 경우가 훨씬 쉽다.
이런 생각으로 시작돼서 발전된 알고리즘이라고 한다.
과정은 다음과 같다.
- 승수의 LSB인 b0의 오른쪽에 값이 0인 1비트 b_-1을 추가한다.
- 오른쪽의 추가 비트 b_-1 부터 1비트씩 왼쪽으로 이동하며 2개의 비트를 묶어 점검한다.
- 승수의 2비트 묶음 값에 따라 아래의 표와 같이 수행한다.

그냥 위의 과정을 따라 해 보면 신기하게도 정확한 연산이 가능하다.

Booth 알고리즘의 장점은 유부호 곱셈도 가능하다는 점이다.
4. 정수의 나눗셈
종이 - 연필 방식의 나눗셈은 아래와 같다.

음.. 특별한 건 없는 것 같다.
문제는 컴퓨터다.
컴퓨터가 나눗셈을 위와 같이 할 수 있을까? 당연히 아니다.
문제는 컴퓨터가 몫이 시작하는 자리를 찾을 수 없다는 것이다.
예를 들어 70 나누기 8을 할 때 7이 8보다 작음을 알려면 컴퓨터는 뺄셈 연산을 실행해야 하고, 뺄셈 연산을 통해 얻은 결과로 몫이 시작할 수 있는지 아닌지를 판단하여 Shift 할 것이다.
이렇게 뺄셈을 통해 나온 결과가 음수라면 원래의 수로 복원시키고, 오른쪽으로 Shift 해서 몫이 시작하는 자리를 찾는 알고리즘을 복원 알고리즘이라 한다.

위의 그림이 아주 잘 설명해 주고 있듯이 뺐을때 음수면 복원시켜놓고(+), 양수면 계산해준다.

위의 그림이 그 과정을 Flow Chart로 나타낸 건데 간단하게만 이해하고 넘어가자.
이제 복원 알고리즘을 이해했다면 복원이라는 과정 때문에 비효율적일 것이라는 것도 예상할 수 있다.
이를 가만히 놔뒀을 리가 없겠죠..?
비복원 알고리즘
정말 간단하게 말하면 복원시키고 쉬프트 하면 오래 걸리니까, 쉬프트 한 곳에다가 더해줄게!이다.
그냥 말장난 같은 알고리즘이지만 조금 더 효율적이라고 한다.

단계수가 많이 줄었음이 보인다..
컴퓨터가 인간과 다르다는 것을 절실히 느낀 챕터였다..
'컴퓨터구조' 카테고리의 다른 글
| Chapter 7. 데이터 경로 연습문제 (0) | 2020.12.07 |
|---|---|
| Chapter 7. 데이터 경로 (2) | 2020.12.06 |
| Chapter 5. 데이터 표현 (0) | 2020.12.03 |
| Chapter 4. 명령어 집합의 분류와 주소 지정 방식 (0) | 2020.12.01 |
| Chapter 3. 명령어 집합 (0) | 2020.11.27 |




