| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- Bit
- 이분탐색
- LCS
- REACT
- 접미사 배열
- 삼성 SW 역량테스트
- BFS
- 삼성SW역량테스트
- r
- 다익스트라
- Air Table
- dp
- 다이나믹 프로그래밍
- 생활코딩
- 고속 푸리에 변환
- 그리디
- 컴퓨터 구조
- Cloud Pub/Sub
- ICPC
- 수학
- 우선순위 큐
- jpa
- Cloud Run
- CI/CD
- JavaScript
- 데이터 분석
- 백준 1753번
- 종만북
- 펜윅 트리
- 시뮬레이션
- Today
- Total
코딩스토리
Chapter 11. 캐시 메모리 본문
# 본 내용은 한국항공대학교 길현영 교수님의 '컴퓨터 구조' 강의 및 컴퓨터 아키텍처(우종정, 한빛 아카데미)를 바탕으로 작성한 글입니다.
교재에는 메모리에 대한 챕터가 따로 있으나 강의에서는 중요한 부분만 보고 넘어갔기 때문에 간단하게 정리하고 캐시로 바로 들어가 보자.
메모리
이전 챕터들에서 메모리에 대한 부분을 어느 정도는? 공부했었다.
기억장치라고도 하며 주기억장치, 보조기억장치로 나뉘며 계층 구조인 것 까지 공부했었던 것 같다.
이제 자세히 살펴보자.
주기억장치 (Main Memory)
주기억장치란 실행될 프로그램과 데이터를 저장하는 기억장치이다.
폰 노이만 아키텍처에서 CPU와 Memory로 나뉜 부분이 가장 중요한 부분 중 하나이다.
(이 부분이 생각보다 큰 단점이어서 탈 노이만 구조의 컴퓨터 구조를 만드는 게 현대 컴퓨터 아키텍처의 목표라고 들었던 것 같아요)
주기억장치는 CPU와 가까운 곳에 위치하며 CPU가 처리할 프로그램과 데이터를 일시적으로 저장한다.
이때 주기억장치는 휘발성 메모리이기 때문에 전원 공급을 중단하면 기억된 내용이 지워진다.
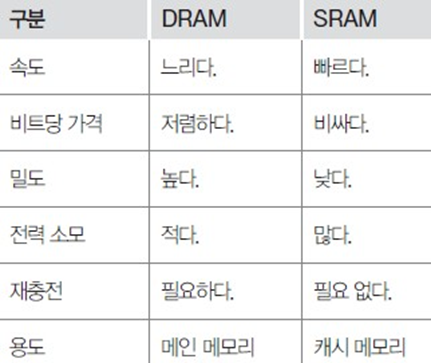
주로 RAM을 의미한다.
(DRAM을 주로 사용한다고 하는데 DRAM, SRAM은 그냥 상식 정도로 알고 있으면 될 듯. 컴활 따는데 도움이 될수도?)
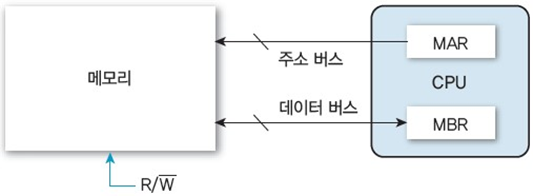
버스가 드디어 나왔다.
내 기억에 1강? 쯤에 잠깐 알아봤었는데 주소 버스와 데이터 버스가 뭔지는 굳이 다시 설명할 필요가 없을 것 같고..
중요한 점은 주소 버스의 비트 수에 따라 몇 개의 주소를 지정 가능한지를 알 수 있다 정도?
(ex. 주소 버스의 비트 수 = 16비트 -> 최대 2^16 = 64K 개의 주소 지정 가능)
주기억장치의 성능과 특징
성능
- 대역폭(bandwidth) : 사이클당 혹은 단위 시간당 전송된 바이트 수
- 지연시간(latency) : 데이터를 얻을 때까지 걸리는 시간
- -> 메모리 접근 시간(Memory Access Time): 데이터 요청부터 그 데이터의 도착까지 시간
- -> 메모리 사이클 시간: 연속된 2개의 데이터를 요청한 시간 간격
특징
- 접근형식 : 저장된 데이터의 접근 순서
- -> 순차접근 저장매체: 처음부터 순서대로 접근 - 자기테이프
- -> 무작위 접근 저장 매체: 데이터의 저장 위치를 직접 검색 – RAM 등
- 가변성: 저장된 데이터를 변경할 수 있는지 여부를 나타내는 속성
- -> 읽기전용 – ROM(Read Only Memory) vs. 읽기쓰기용
- 휘발성: 전원을 차단했을 때 저장된 데이터가 증발하는지 여부에 대한 속성
- -> 휘발성 – RAM vs. 비휘발성 – ROM
성능과 특징이라고 말했지만 사실 이미 다 알고 있는 것들일 것이다.
메모리의 계층 구조
속도와 용량이 서로 다른 다수의 계층으로 구성된 메모리 구조를 의미한다.
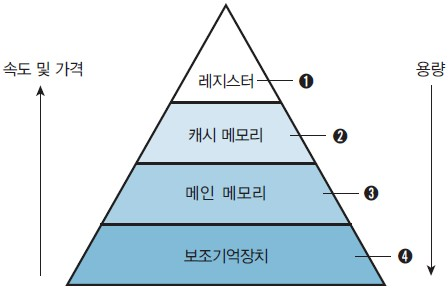
위 그림을 보면 이제는 캐시 메모리 빼고는 대부분 알았을 것이다.
계층 구조에서 꼭 알아야 할 점이 있다.
바로 인접한 두 계층 사이에서만 데이터 전송이 발생한다는 점이다!
(내가 웬만하면 빨간색 잘 안 쓰는데..)
이 점이 왜 중요하냐면 레지스터가 메인 메모리에 직접적으로 접근하지 못한다는 말은 반드시 캐시 메모리를 거쳐서 접근해야 된다는 말이다. 그만큼 시간이 더 걸린다는 말이다.
(많이 쓰는 정보들은 CPU와 가장 가까운 저장장치에 저장해놓으면 굳이 메인 메모리까지 가지 않아도 된다)
어.. 그냥 중요해요!
추가적으로 소용량의 빠른 메모리(레지스터)를 CPU에 가깝게 배치하고, 느리지만 대용량의 메모리(보조기억장치)를 CPU에 멀리 배치한 메모리 계층 구조가 저렴하고 효율적이라고 한다.
캐시 메모리
위에서 캐시 메모리(이제부터는 캐시라고 할게요)를 보면 계층 구조에서 꽤? 위에 있는 것을 알 수 있다.
그 뜻은 당연히 빠르고 용량이 적다는 의미다.
캐시는 CPU와 메모리 사이의 속도 차이를 줄이기 위한 고속 메모리이다.
고속 메모리인 만큼 비싸고, 용량이 작으며 컴퓨터 성능에 영향을 미친다.
투명성 : 프로그래머는 캐시를 조작할 수 있는 명령어가 없다
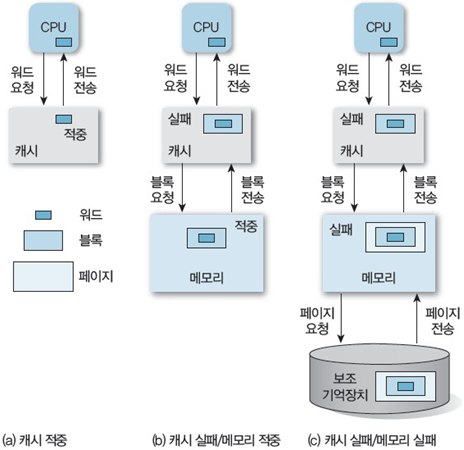
위 그림을 잘 이해해야 한다.
CPU는 워드 단위로 일을 처리한다.
당연히 메모리에 워드 단위의 정보를 요청할 것이다.
이때 메모리와 CPU사이에 캐시가 존재한다.
만약 캐시에 CPU가 원하는 정보가 있다면 적중(Hit)이라 하며 그 정보를 CPU로 보내준다.
만약 캐시에 CPU가 원하는 정보가 없다면 실패(Miss)라 하며 메모리로 원하는 정보를 요청한다.
이때 메모리는 블록 단위기 때문에 블록을 요청하고 받아온다.
보조기억장치까지 가면 페이지 단위라고 하는데 이건 그냥 알아만 두자.
아까 빨간색 친 이유가 여기에 있다.
적중에 실패하면 결국 다음 저장장치, 그다음 저장장치로 가야 한다는 것이다.
적중률 : 메모리 참조에 대한 캐시 성능

Tag Memory
캐시는 고속 메모리인 만큼 메인 메모리보다 작다.
따라서 각 캐시 엔트리에는 메모리 내 여러 주소값 블록들이 적재되어야 한다.
태그 메모리는 캐시 메모리가 어떤 데이터를 포함하는지를 관리하기 위해 사용한다.
지금은 이해가 잘 안되는데 밑에서 조금 더 자세히 살펴보자.
캐시 메모리의 용량을 얘기할 때는 주로 태그 메모리는 빼고, 데이터 메모리 용량만을 의미한다고 한다.
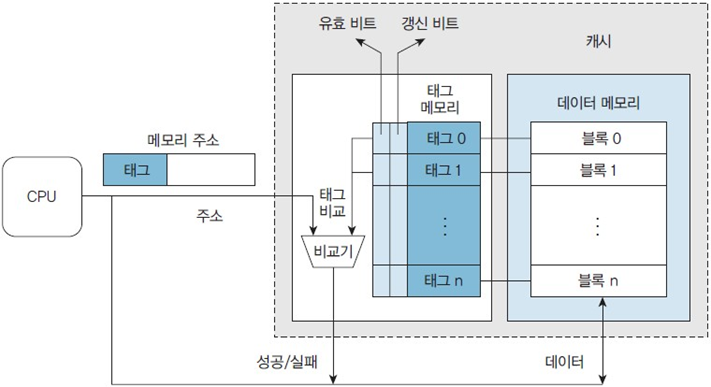
태그 메모리의 각 엔트리는 캐시의 데이터 메모리의 블록과 대응된다(쌍을 이룬다. 위 그림처럼).
(블록은 워드의 집합으로 데이터 메모리 내 기본단위이다. 캐시와 메모리의 데이터 전송의 기본 단위이기도 함)
태그 메모리는 최소한 세 가지 정보를 포함한다.
- 태그(tag) : CPU가 요청한 블록을 탐색하는 데 사용하는 주소 정보의 일부
- -> 캐시 블록 주소에서 인덱스로 사용되지 않는 주소의 윗부분
- 유효 비트(valid bit) : 캐시 블록이 유효한 데이터인지 아닌지를 표시
- -> 컴퓨터가 부팅될 때 모든 유효 비트를 무효로 초기화
- 갱신 비트(dirty bit) : 메모리에서 캐시로 블록을 가져온 후 CPU가 블록을 수정했는지 표시
또한 태그 메모리는 CPU 주소와 태그를 비교하는 비교기(comparator)도 가지고 있다.
캐시에 필요한 전략과 설계 논점
캐시 메모리는 속도가 중요하므로 대부분 HW로 구현된다.
캐시를 사용하는 데에는 블록 사상 방식, 블록 교체 방식, 블록 갱신 방식 등 여러 가지 방식이 있다.
블록 사상 방식
사상 = mapping이다.
(나는 영어를 싫어하지만? 사상 방식 보단 mapping 이 더 이해가 쉬운 것 같다)
즉 블록을 메모리에서 가져와서 캐시에 어떻게, 어디다 가져다 놓을건지를 정하는 것이다.
블록 사상이 필요한 이유는 캐시가 메모리보다 용량이 작기 때문에 다수의 메모리 블록이 동일한 캐시 블록에 사상된다.
블록 사상 방식에는 크게 3가지가 있다.
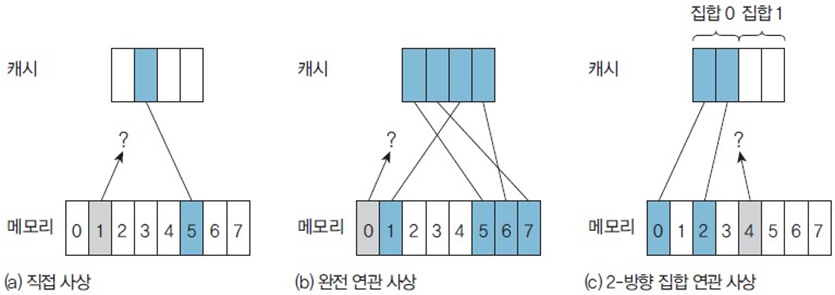
- 직접 사상(direct mapping) : 메모리 블록을 정해진 하나의 캐시 블록에만 사상할 수 있다.
- 완전 연관 사상(fully-associative mapping) : 메모리 블록을 어떤 캐시 블록에도 사상
- 집합 연관 사상(set-associative mapping) : 직접 사상과 완전 연관 사상을 절충하여, 메모리 블록을 정해진 블록의 집합 내 어디든 사상
만약 시스템이 아래와 같다고 가정하자.
메모리 크기(512 Byte), 캐시 크기(128 Byte), 블록 크기(16 Byte), 워드 크기(4 Byte)
이를 통해 알아낼 수 있는 정보들은 아래와 같다.
-> 메모리 = 2^9 -> 메모리 주소는 9bit 필요
-> 캐시 = 2^7 -> 캐시 주소는 7bit 필요
-> 메모리(512)에 블록(16)이 총 32개 들어갈 수 있음
-> 즉 메모리 블록 주소는 2^5개 필요 -> 5bit
-> 캐시(128)에는 블록(16)이 8개 들어갈 수 있음
-> 즉 캐시 블록 주소는 2^3개 필요 -> 3bit
-> 블록은 16byte, 즉 2^4 이므로 블록 오프셋은 4bit
( 블록 내에서 1바이트 선택하려면 블록 오프셋 4비트를 사용하고, 1 워드를 선택하려면 블록 오프셋의 상위 2비트를 사용 -> 이 말이 이해가 잘 안 갔는데 워드가 4byte라는 건 블록에 4개의 워드가 존재, 따라서 4bit 중 상위 2bit(2^2개 표현 가능)만 사용하여도 블록 내의 모든 워드를 표현할 수 있다는 것이다.)
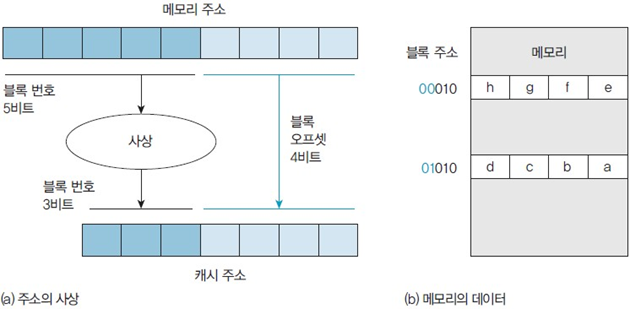
직접 사상 방식
직접 사상 방식은 modulo(나머지, mod) 연산을 통해 메모리 블록을 정해진 캐시 블록에만 사상시킨다.
즉 메모리의 블록들은 캐시에 들어올 때 자리가 이미 정해져 있다는 것이다.
위에서 가정했던 시스템이라고 생각해보면,
캐시에는 8개의 블록이 저장 가능하다.
따라서 메모리의 블록 번호를 8로 나눈 나머지(mod) 값이 블록 번호가 된다.
(이 뜻인즉슨 메모리 블록 번호에 따라 이미 캐시에 들어갈 장소는 정해져 있다는 거겠죠?)
메모리 블록 주소는 5bit이고, 5bit를 8로 나눈 나머지만 쓰겠다는 말은 하위 3bit만 쓰겠다는 말과 동일하다.
(이건 간단한 수학적 논리)
이때 보면 하위 3bit만 쓰기 때문에 캐시의 같은 공간에 들어가야 하는 블록들이 생긴다.
(계산해보면 각각의 공간마다 정확히 4개의 블록이 겹치겠네요)
그렇다면 이렇게 겹치는 블록들이 연달아서 사상되어야 한다면.. 좋지 않을 것 같다.
그럼 데이터 메모리 주소는 9bit인데 블록 번호가 3bit고 블록 오프셋이 4bit면 나머지 2bit는 뭘까?
바로 태그 필드이다.
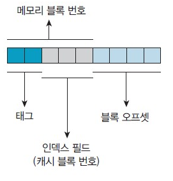
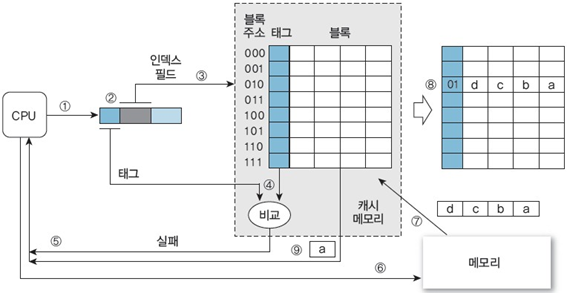
이제 실제로 CPU가 데이터를 어떻게 받아오는지 살펴보자.
1. 주소 010100000의 데이터 a 참조 (캐시 초기화 단계)
① CPU가 주소 010100000을 생성하여 캐시 메모리에 데이터를 요청
② 캐시는 주소를 CPU 태그(01), 인덱스(010), 블록 오프셋(0000)으로 분할
③ 인덱스 필드(010)가 가리키는 캐시의 태그를 추출
④ CPU 태그와 캐시 태그를 비교
⑤ 유효 비트가 0이므로 캐시 실패 발생 (CPU에 알림)
⑥ CPU는 메모리에 동일한 주소를 보내어 데이터를 요청
⑦ 메모리는 데이터 a가 있는 메모리 블록(주소: 01010)을 복사하여 캐시 메모리로 전송
⑧ 메모리 블록을 인덱스 필드(010)가 가리키는 캐시 블록으로 사상하고 캐시 태그를 01로 갱신한 뒤, 유효 비트를 1로 설정
⑨ 블록 오프셋(0000)을 사용하여 캐시 블록에서 데이터 a를 추출하고 CPU에 전송
차근차근 읽어보면 별거 없다.
그냥 Hit와 Miss를 구분하고, 주소를 bit로 잘 나누고, 나눈 bit가 뭘 뜻하는지만 알고 있다면 어렵지 않게 이해할 수 있다.
2. 주소 010100100에 있는 데이터 b를 참조
① ~ ④ 데이터 a를 참조할 때와 동일한 방식으로 수행
⑤ 유효 비트가 1이며 두 태그가 일치하므로 캐시 적중
⑥ 블록 오프셋(0100)을 사용하여 캐시 블록에서 데이터 b를 추출하고 CPU에 전송
이미 가져온 블록 안에 원하는 워드 b가 있기 때문에 빠르게 CPU에서 참조가 가능하다.
3. 주소 000100000에 있는 데이터 e 참조
동일 캐시 블록 사용(데이터 a와 e의 메모리 블록은 하위 3bit가 동일)에 따른 충돌 발생
-> 새로운 블록이 들어와야 하기 때문에 기존 캐시에 있던 블록을 삭제해야 되는 상황이 발생
① ~ ④ 데이터 a를 참조할 때와 유사하게 수행
⑤ 두 태그가 일치하지 않으므로 CPU에 캐시 실패라고 알림 -> 태그 비교
⑥ CPU는 메모리에 동일한 주소를 보내어 데이터를 요청
⑦ e가 있는 메모리 블록(주소: 00010)에 접근: 데이터 e를 포함한 블록을 사상할 캐시 블록에는 데이터 a를 가진 다른 블록(주소: 01010)이 존재하므로, 데이터 a를 포함하는 캐시 블록의 갱신 여부를 파악하고 쓰기정책에 맞게 처리
⑧ e를 포함하는 메모리 블록(주소: 00010)을 캐시 블록(010)으로 사상하고 태그를 00으로 갱신
⑨ 블록 오프셋(0000)을 사용하여 캐시 블록에서 데이터 e를 추출하고 CPU에 전송
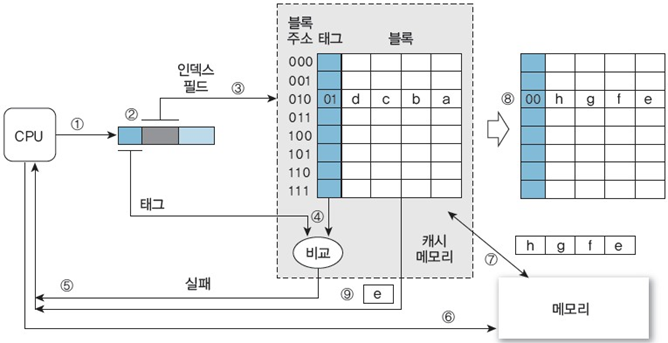
직접 사상의 장단점
장점
태그의 길이가 짧다
CPU 태그를 하나의 캐시 태그와 비교하기 때문에 하나의 비교기만 있으면 가능
메모리 블록이 사상될 캐시 위치가 정해져 있어, 교체 방식이 필요 없음
∴ 따라서 하드웨어 구현이 단순하고 접근 속도가 빠르다.
단점
적중률이 저조
특히 동일한 캐시 블록에 사상되는 다른 메모리 블록을 번갈아 참조할 때 캐시 블록에 심각한 충돌이 발생하여 적중률이 급격히 낮음 -> 위의 경우 a, e, a, e 이 순서대로 참조하면 계속 Miss가 날 것이다.
∴ 그래서 대용량 캐시 메모리일 경우에만 주로 직접 사상 방식을 이용
완전 연관 사상
완전 연관 사상 방식은 메모리 블록을 어떤 캐시 블록에도 사상 가능한 방식이다.
즉 캐시에 빈 공간이 있으면 그곳에 사상시킨다는 말이다.
가장 큰 특징은 인덱스 필드가 없다는 것이다.
메모리 블록 번호 모두가 태그로 사용된다. (위의 가정의 경우 5bit 전체가 태그 필드란 말임)
1. 주소 0101000000에 있는 데이터 a를 참조 (캐시 초기화 단계)
① CPU가 주소 010100000을 생성하여 캐시 메모리에 데이터를 요청
② 캐시 메모리는 주소를 CPU 태그(01010)와 블록 오프셋(0000)으로 분할
③ CPU 태그와 모든 캐시 태그를 비교
④ 유효 비트가 0이므로 CPU에 캐시 실패라고 알림
⑤ CPU는 메모리에 동일한 주소를 보내어 데이터를 요청
⑥ 데이터 a가 있는 메모리 블록(01010)을 복제하여 캐시 메모리에 전송
⑦ 메모리 블록을 임의의 캐시 블록에 사상: 어느 빈 블록이라도 상관없지만 첫 번째 빈 캐시 블록으로 사상한다면, 캐시 태그를 01010으로 갱신하고, 유효 비트를 1로 설정
⑧ 블록 오프셋(0000)을 사용하여 캐시 블록에서 데이터 a를 추출하고 CPU에 전송
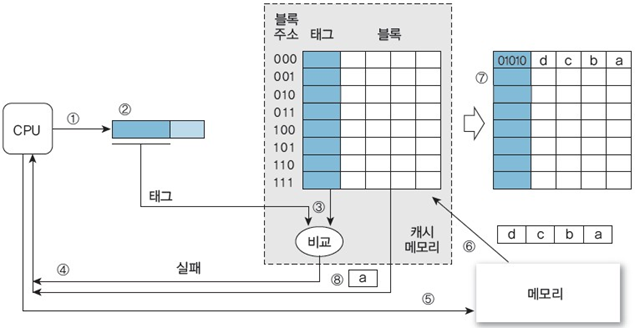
2. 주소 010100100에 있는 데이터 b를 참조
① ~ ③ 데이터 a를 참조할 때와 유사하게 수행
④ 유효 비트가 1이며, 일치하는 태그(01010)가 있으므로 캐시 적중
⑤ 블록 오프셋(0100)을 사용하여 캐시 블록에서 데이터 b를 추출하고 CPU에 전송
3. 주소 000100000에 있는 데이터 e 참조
① ~ ③ 데이터 a를 참조할 때와 유사하게 수행
④ 일치하는 태그가 없으므로 CPU에 캐시 실패라고 알림
⑤ CPU는 메모리에 동일한 주소를 보내어 데이터를 요청
⑥ 데이터 e가 있는 메모리 블록(00010)에 접근하여 캐시 메모리로 가져옴
⑦ 메모리 블록을 비어 있는 임의의 캐시 블록으로 사상 : 편의상 두 번째 캐시 블록으로 메모리 블록을 사상하고, 대응하는 두 번째 캐시 블록의 태그를 00010으로 갱신
(만약 빈 캐시 블록이 없으면 캐시 교체 방식과 쓰기 정책에 따라 사용 중인 블록을 처리)
⑧ 블록 오프셋(0000)을 사용하여 캐시 블록에서 데이터 e를 추출하고 CPU에 전송
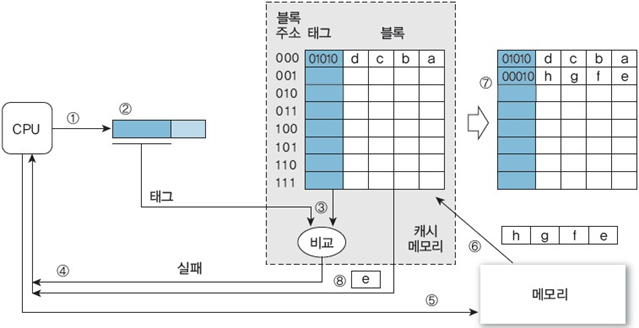
직접 사상 방식과는 다른 걸 알 수 있다.
비어 있으면 그곳에 넣으면 된다.
완전 연관 사상의 장단점
장점
직접 연관 사상보다 적중률이 높음 (시간적 locality)
단점
CPU가 요청한 태그를 모든 캐시 태그와 병렬로 비교해야 하므로 8개의 비교기가 필요
태그의 길이도 길다.
직접 사상에 비해 속도가 느리고, 추가 하드웨어 필요
∴ 고가(빠르고 정확)의 연관 메모리를 사용
집합 연관 방식
집합 연관 방식은 직접 사상 방식과 완전 연관 사상 방식을 합친 방식이다.
정해진 장소(직접 사상) 내 어느 블록에나(완전 연관 사상) 위치 가능하다.
즉 캐시를 일정 개수의 집합으로 나누어 놓고 그 집합에서는 비어있는 한 어느 곳에나 위치가 가능하다.
이때 몇 개의 집합으로 나누는지에 따라 n-방향 집합 연관 사상이라고 부른다.
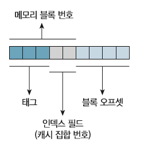
만약 2-방향 집합 연관 사상이라면
위의 그림처럼 인덱스 필드(캐시 집합 번호)가 2bit가 필요할 것이다.
(이유는 일단 캐시는 가정에 의해 8개의 블록을 담는다. 이때 2-방향 이므로 각 집합은 2개의 블록씩을, 즉 4개의 집합이 캐시에 있다는 것이다.
쉽게 생각해보면 4개의 집합 중 어디에 담을지를 표현하려면 2bit가 필요한 건 당연하겠죠..?)
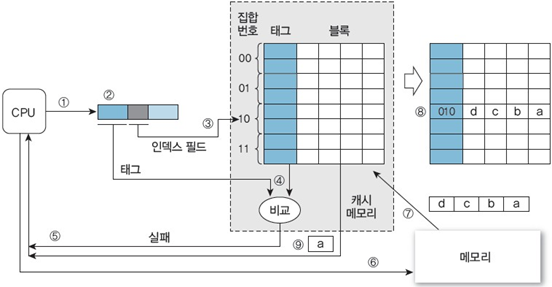
1. 주소 010100000에 있는 데이터 a를 참조 (캐시 초기화 단계)
① CPU가 주소 010100000을 생성하여 캐시 메모리에 데이터를 요청
② 캐시 메모리는 주소를 CPU 태그(010), 인덱스(10), 블록 오프셋(0000)으로 분할
③ 인덱스 필드가 가리키는 캐시 메모리의 태그 2개를 추출 -> 처음엔 헷갈렸는데 잘 보면 2 방향이므로 각 집합에는 2개의 태그가 존재하는 게 맞음. 즉 각 집합의 모든 태그들을 추출한다는 말과 동일
④ CPU 태그와 2개의 캐시 태그를 비교
⑤ 캐시 메모리가 초기 상태이므로 유효 비트가 0이므로 CPU에 캐시 실패라고 알림
⑥ CPU는 메모리에 동일한 주소를 보내어 데이터를 요청
⑦ 데이터 a가 있는 메모리 블록(01010)을 복제하여 캐시 메모리에 전송
⑧ 메모리 블록을 인덱스 필드가 지시하는 캐시 집합에 사상하고, 캐시 태그를 010로, 유효 비트를 1로 설정
(하나의 캐시 집합이 2개의 블록이므로, 편의상 첫 번째 빈 캐시 블록에 사상)
⑨ 블록 오프셋(0000)을 사용하여 캐시 블록에서 데이터 a를 추출하고 CPU에 전송
2. 주소 010100100에 있는 데이터 b를 참조
① ~ ④ 데이터 a를 참조할 때와 유사하게 수행
⑤ 2개의 캐시 태그 중 하나가 CPU 태그와 일치하므로 캐시 적중
⑥ 블록 오프셋(0100)을 사용하여 캐시 블록에서 데이터 b를 추출하고 CPU에 전송
3. 주소 000100000에 있는 데이터 e를 참조
① ~ ④ 데이터 a를 참조할 때와 동일한 방식으로 수행
⑤ 일치하는 캐시 태그가 없으므로 CPU에 캐시 실패라고 알림
⑥ CPU는 메모리에 동일한 주소를 보내어 데이터를 요청
⑦ 데이터 e가 있는 메모리 블록(00010)을 복제하여 캐시 메모리로 가져옴
⑧ 데이터 e를 포함한 메모리 블록을 인덱스 필드(10)가 지시하는 캐시 집합 내 빈 블록으로도 사상하고, 캐시 태그를 000으로 갱신 -> 만약 해당 캐시 집합에 빈 캐시 블록이 없으면, 캐시 교체 방식에 따라 블록 하나를 축출하고, 또한 쓰기 정책에 따라 메모리의 내용을 캐시의 내용과 일치
⑨ 블록 오프셋(0000)을 사용하여 캐시 블록에서 데이터 e를 추출하고 CPU에 전송
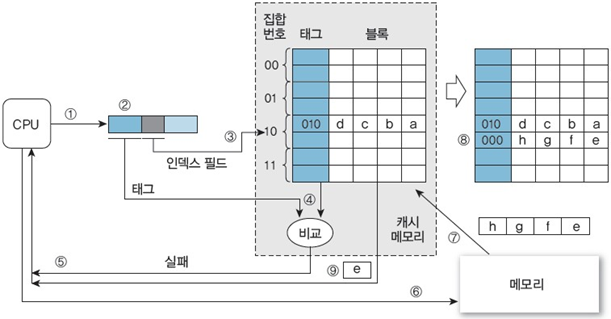
가장 큰 차이점은 두 블록 모두 캐시에 들어있다는 점이다.
집합 연관 사상 방식의 특징
완전 연관 사상과 직접 사상의 혼합 형태
전체 태그 대신 일부 태그에 대해 연관 탐색을 수행
적은 개수의 비교기가 필요
태그의 길이도 짧음
∴ 완전 연관 사상에 비해 비용이 저렴하고 속도도 빠른 편
∴ 완전 연관 사상보다 적중률이 떨어지지만 직접 사상보다는 적중률이 높은 편
직접 사상과 완전 연관 사상은 집합 연관 사상의 일종
만약 하나의 캐시 집합에 1개 블록만 있다면? 직접 사상
전체 캐시 블록이 하나의 캐시 집합이라면? (==예제에서 캐시 집합의 크기가 8개 블록) 완전) 연관 사상
-> 쉽게 말해 n을 줄이거나 늘리는 거에 따라 직접 사상 또는 완전 연관 사상이 될 수 있다는 말이다.
블록 교체와 블록 갱신
위에서 블록 사상 방식 과정을 보면서 중간중간에 블록 교체와 블록 갱신 방식에 따라 진행한다고 하였다.
이제 블록 교체와 블록 갱신에 대해서 살펴보자.
블록 교체 방식
말 그대로 캐시 공간이 없어서 캐시 블록을 비워야 할 때 어떤 캐시 블록을 비울 건지를 결정하는 방식이다.
블록 교체 전략에는 여러 가지 방법이 있다.
Belady의 MIN 알고리즘
- 이상적인 블록 교체 방식으로 가장 오랫동안 참조되지 않을 블록을 교체
- 미래 예측이 필요
최소 최근 사용(LRU, least recently used) 방식
- MIN 알고리즘에 근접할 정도의 최고 적중률을 보임
- 모든 블록에 대해 최근에 참조된 정보를 포함해야 하므로 구현 비용이 높음
무작위 (random) 방식
- 임의의 캐시 블록을 선택하여 축출함으로써 캐시 메모리 공간을 준비
- 효율성은 보장하기 어렵지만 구현 비용이 저렴하고 간단
선입 선출(FIFO, first-in first-out) 방식
- 캐시 메모리에 먼저 적재된 블록을 먼저 축출하므로써 캐시 메모리 공간을 준비
- 효율성을 보장하기 어렵지만 time locality 기반으로 구현 비용이 저렴
음.. 그냥 잘 읽어보고 넘어가자.
블록 갱신 방식
캐시가 존재하는 컴퓨터라면 데이터는 메모리와 캐시 이 두 곳에 동시에 존재할 수 있다.
같은 데이터라면 어느 곳에 있든 같은 정보를 가지고 있어야 한다.
하지만 캐시를 사용하게 되면 동일 블록(같은 주소)에 다른 값을 갖는 현상이 발생한다.
주로 데이터를 캐시에만 Write 하고 메인 메모리에는 쓰지 않은 경우에 발생한다.
(캐시 시스템에서는 캐시의 데이터에 R/W 연산을 우선적으로 수행하기 때문)
블록 갱신 방식은 캐시의 내용을 메모리와 일치시키는 시점에 따라 두 가지로 나뉜다.
즉시 쓰기
- Write 연산시, 항상 데이터를 메모리와 캐시에 같이 쓰는 방법
- 성능 저하
- -> 만약 쓰기 연산은 최소 100개의 clock cycles 사용하고 명령어의 10%가 store라 가정하자. 캐시 실패가 없는 경우의
- -> CPI=1이라 가정하면, CPI=1.0 + 100*10% = 11
- 쓰기 버퍼(Write buffer) 사용 : 쓰기 버퍼는 메모리에 쓰일 데이터를 저장
- 데이터 캐시와 쓰기 버퍼에 쓰고 난 후, 프로세서는 수행을 계속함
- Write 연산이 폭주하여 쓰기 버퍼가 모두 차 있으면? 지연 발생. 가능한 큰 버퍼 확보
당연한 얘기지만 이 경우 성능 저하가 심하다.
메모리까지 가는 게 오래 걸려서 캐시를 만들어다 갖고 왔더니 자꾸 메모리에 방문한다.
쓰기 버퍼를 통해서 완화시키기는 하지만 이마저도 큰 버퍼가 필요하다.
나중 쓰기
- 쓰기 발생 시 새로운 값은 캐시 내 블록에만 쓰고, 나중에 캐시에서 나가는 블록이 쓰기연산에 의해 수정되었을 경우, 다음 하위 레벨의 메모리에 데이터 갱신
- 갱신 비트 사용 : 캐시블록의 수정 여부를 표시
- 속도가 빠르고 메모리 트래픽 감소
- 즉시 쓰기보다 설계/구현이 복잡
- -> 캐시-메모리 데이터 불일치 문제 - 입출력 장치가 데이터를 요구했을 때, 어느 것이 유효한 데이터인지 모름
- -> CPU와 캐시에 문제 발생 시,, 데이터 복구가 어려움
즉 갱신 비트를 사용하여 블록이 나갈 때만 메모리까지 갱신하겠다는 말이다.
속도가 빠르다는 건 지금까지 봐서 알겠지만 설계/구현하기 복잡하다는 것..
데이터 복구가 어렵다는 것도 큰 단점이다.
캐시 메모리를 통한 성능 향상
이제 캐시를 사용해서 성능 향상을 할 수 있다는 것을 알았다.
캐시 성능 향상을 하려면 캐시 실패율을 낮추어야 한다.
캐시 실패의 유형은 다음과 같다.
- 강제 실패 (Compulsory Miss) : 해당 메모리 블록의 최초 접근에 의한 캐시 미스
- -> 블록 크기를 크게 하거나, 가장 접근 가능성이 큰 블록의 prefetch로 감소 노력
- 용량 실패 (Capacity Miss) : 매키 메모리의 유한한 용량 때문에 발생
- -> 블록 교체 후 다시 그 블록을 가져올 때 발생 (캐시 용량 < 프로그램 크기)
- 충돌 실패 (Collission Miss) : 다수의 블록이 동일한 집합/블록에 사상됨으로써 발생
- -> 집합연관 사상이나 직접 사상의 경우 발생. (Q. 완전연관사상에서는완전 연관 사상에서는? -> 발생 X)
캐시 성능의 평가기준은 캐시 적중률과 캐시 유효 접근 시간으로 판단한다.
적중률은 앞에서 공부했고, 유효 접근 시간은 다음과 같다.
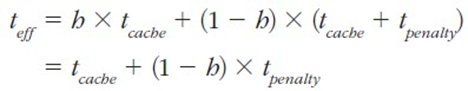
h : 캐시메모리 적중률(%)
t_cache : 캐시메모리 적중시 걸린 접근 시간(time);
t_penalty : 캐시메모리 실패시 걸린 시간(time) = 하위 메모리에서 해당 블록을 갖고오는데 걸리는 시간

# t_memory : 메모리 접근 시간; t_transfer : 블록 전송 시간
거의 다 왔다.. 힘내자
이제 캐시 메모리의 성능을 개선하려면 어떻게 해야 되는지 알았다.
1. 실패율 down : 3C를 줄이자
- 강제 실패를 감소시킬려면? 블록을 크게 또는 효과적인 prefetching
- 충돌 실패를 감소시킬려면? 연관도를 높이기
- 용량 실패를 감소시킬려면? 캐시 용량을 크게
- 컴파일러를 통한 프로그램의 메모리 사용 최적화 등
2. 실패 페널티 down : 메모리 액세스 타임을 줄이자
- 메모리 대역폭 향상, 블록 크기 줄이기, 요청한 워드 우선 전송방식 등
3. 적중 시간 down : 캐시 액세스 타임을 줄이자
- 캐시의 소용량화, 직접 사상 등
위의 내용을 자세히 보면 알겠지만 각각의 해결책이 독립적이지 않다.
블록 크기
증가시 : (+) 시공간적 지역성 상승으로 적중률 상승, 블록 개수의 감소로 tag 메모리 양 감소
(-) 메모리 액세스 시간이 증가하여 캐시 미스에 따른 패널티 증가, 블록 개수의 감소로 시간적 지역성 감소 (특 히, 작은 캐시인 경우)
감소시 : (+) 메모리 액세스 시간이 감소하여, 캐시 미스에 따른 패널티 감소
(-) 공간적 지역성의 감소로 적중률 감소 (특히, 초기 강제 실패 증가), 블록 개수의 증가로 tag 메모리 양 증가
공간적 지역성 상승이란 prefetching과 같이 a를 가져왔는데 b도 딸려와서 좋다는 것이다.
tag 메모리는 블록 크기에 반비례한다. (16개의 블록이 들어가 있는 게 4개의 블록이 들어가 있는 것보다 tag가 많이 필요)
증가 시와 감소 시 장점과 단점이 서로 반대임을 확인할 수 있다.
즉 무조건 증가시키거나 감소시키는 게 좋은 게 아니라는 것이다.
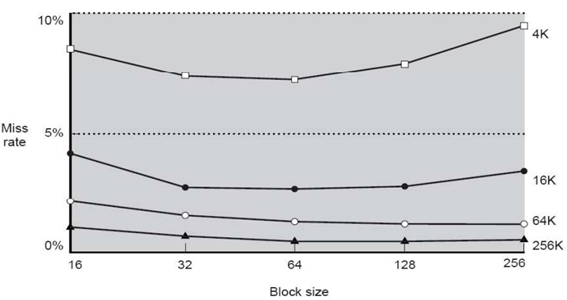
위 그림에서 보다시피 블록 사이즈가 무작정 크다고 Miss rate가 낮아지는 것은 아니다.
(실제로 블록 사이즈가 64byte일 때가 가장 좋다는 것을 알 수 있다.)
캐시 용량
증가시: (+) 공간적/시간적 지역성의 상승으로 적중률 증가, 다양한 블록 크기 및 사상 방식등의 활용이 실제적으로 가능
(-) 하드웨어의 부담이 커짐
감소시: (+) 하드웨어의 부담 감소
(-) 용량 실패와 충돌 실패의 증가, 블록 크기나 사상 방식 선택의 제약 등
너무너무 당연한 말들이다.
캐시 용량이 커지면 그만큼 캐시에 많은 데이터를 담고 있기 때문에 적중률이 증가하지만 그걸 설계/구현하는 게 어렵고 그만큼 HW의 부담이 커질 수밖에 없다.
캐시 연관도
증가시: (+) 적중률이 전반적으로 증가
(-) 캐시 메모리 구성의 복잡도 증가로, 적중 시간이 길어지고 비용도 증가, 용량이 작은 캐시의 경우에는 부적합
감소시: (+) 작은 캐시의 경우 적합
연관도는 몇 방향 집합 연관 사상인지를 나타내는 것이다.
즉 집합의 크기가 커질수록 여러 종류의 데이터를 다양하게 담고 있기 때문에 적중률이 증가할 순 있으나 적중 시간이 길어진다. (태그가 많아지니까..?)
위의 내용들을 간단하게 정리하면 아래와 같다.
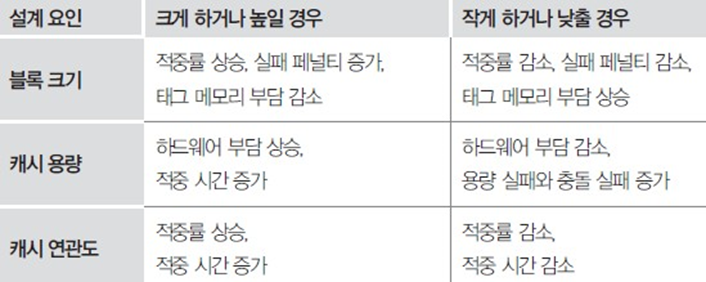
다단계 캐시
이렇게 좋은 캐시를 하나만 쓸 수 없지요
현대 컴퓨터들은 다단계 캐시로, 단계별로 캐시를 가지고 있어 실패 페널티를 만회한다.
- 1차 캐시(primary cache): 작지만 빠름
- 2차 캐시(secondary cache): 1차 캐시에 비해 크지만 느림 (메인 메모리보다는 빠름)
- 고성능 프로세서들은 3차 캐시도 보유
1차 캐시는 CPU가 데이터를 가져올 때 무조건 반드시 한 번씩 거치기 때문에 Clock cycle이 짧아지도록 적중 시 액세스타임 최소화에 중점을 둔다. 또한 블록의 크기를 작게 하여 실패 손실을 최소화한다.
2차 캐시는 1차 캐시보다는 덜 방문하기 때문에 메모리 접근을 줄이기 위해, 실패율 최소화에 중점을 둔다.
캐시가 하나 있는 것보다 전체 성능이 좋아지므로, (1차 캐시에 비해)액세스 타임에 대한 부담이 덜해진다.
1차 캐시와 반대로 캐시 용량과 블록 크기를 크게 만든다.
실습 풀이도 한번 해보려고 했는데 너무 피곤해서 다음에 하는 걸로.. (다음 주 시험인데 다음에 한다고?)
정리하는데 제일 오래 걸린 챕터인 것 같다. 왜지..?
어쨌든 중요한 건 캐시 짱좋다!
'컴퓨터구조' 카테고리의 다른 글
| Chapter 9. 파이프라이닝 연습문제 (0) | 2020.12.17 |
|---|---|
| Chapter 9. 파이프라이닝 (0) | 2020.12.17 |
| Chapter 7. 데이터 경로 연습문제 (0) | 2020.12.07 |
| Chapter 7. 데이터 경로 (2) | 2020.12.06 |
| Chapter 6. 연산장치 (0) | 2020.12.05 |



